范数norm
维基搜索norm得到的结果数学部分摘录如下：
In mathematics：
- Norm (mathematics), a map that assigns a length or size to a mathematical object, e.g.:
- Vector norm, a map that assigns a length or size to any vector in a vector space
- Matrix norm, a map that assigns a length or size to a matrix
- Operator norm, a map that assigns a length or size to any operator in a function space
- Norm (abelian group), a map that assigns a length or size to any element of an abelian group
- Field norm, a map in algebraic number theory and Galois theory that generalizes the usual distance norm
- Ideal norm, the ideal-theoretic generalization of the field norm
- Norm (group), a certain subgroup of a group
- Norm (map), a map from a pointset into the ordinals inducing a prewellordering
- Norm group, a group in class field theory that is the image of the multiplicative group of a field
- Norm function, a term in the study of Euclidean domains, sometimes used in place of "Euclidean function"
下面仅介绍我预测数据分析可能用到的向量范数和矩阵范数。
1 Vector norm向量范数
1.1 Definition定义
Given a vector space $V$ over a subfield $F$ of the complex numbers, a norm on $V$ is a nonnegative-valued scalar function $p: V \rightarrow [0,+\infty)$with the following properties:给定一个向量空间$V$和复数子域$F$，在$V$上的范数是一个非负标量方程：$p: V \rightarrow [0,+\infty)$，此方程有如下特性：
For all $a \in F$ and all $\vec{u}, \vec{v} \in V$: 对任意$a \in F$和任意$\vec{u}, \vec{v} \in V$：
$p(\vec{u} + \vec{u}) ≤ p(\vec{u}) + p(\vec{v})$(being subadditive or satisfying the triangle inequality).是次加性的也就是满足三角不等式。$p(a\vec{v}) = |a| p(\vec{v})$(being absolutely homogeneous or absolutely scalable).是绝对同构的也就是绝对可伸缩。- If
$p(\vec{v}) = 0$then$\vec{v}=\vec{0}$(being positive definite or being point-separating).如果$p(\vec{v}) = 0$那么$\vec{v}=\vec{0}$（正定的或点分离的）。
A seminorm on $V$ is a function $p : V → R$ with the properties 1 and 2 above. $V$上的半范数是方程$p : V → R$，满足上面的特性1和特性2。
Every vector space $V$ with seminorm $p$ induces a normed space $V/W$, called the quotient space, where $W$ is the subspace of $V$ consisting of all vectors $\vec{v}$ in $V$ with $p(\vec{v}) = 0$. The induced norm on $V/W$ is defined by:每个向量空间$V$和半范数$p$诱导一个范数化的空间$V/W$，叫做商空间，其中$W$是$V$的子空间，$W$含有$V$中所有$p(\vec{v}) = 0$（范数为0）的向量。引入的$V/W$上的范数定义如下。
$$p(W + \vec{v}) = p(\vec{v})$$
Two norms (or seminorms) $p$ and $q$ on a vector space $V$ are equivalent if there exist two real constants $c$ and $C$, with $c > 0$, such that
for every vector $\vec{v}$ in $V$, one has that: $c q(\vec{v}) ≤ p(\vec{v}) ≤ C q(\vec{v})$.向量空间V上的两个范数(或半范数)p和q是等价的，如果存在两个实常数$c$和$C$，且$c > 0$，对于在$V$的每个向量$\vec{v}$，有$c q(\vec{v}) ≤ p(\vec{v}) ≤ C q(\vec{v})$。
A topological vector space is called normable (seminormable) if the topology of the space can be induced by a norm (seminorm).如果空间的拓扑可以由范数(半范数)诱导，则拓扑向量空间称为可规范(半可规范)。
1.2 Examples举例
1.2.1 Euclidean norm
(special case of:p-norm)
可以定义到向量中的值含有复数，但由于数据分析不会涉及到复数，以下叙述仅考虑实数：
$$\left\|\vec{x}\right\|_2:=\sqrt{\sum_{i=1}^{n}{x_i^2}}$$
也可写成
$$\left\|\vec{x}\right\|_2:=\sqrt{\vec{x}^T\vec{x}}$$
1.2.2 Taxicab norm or Manhattan norm
(special case of:p-norm)
$$\left\|\vec{x}\right\|_1:=\sum_{i=1}^{n}{|x_i|}$$
1.2.3 p-norm
$$\left\|\vec{x}\right\|_p:=\left(\sum_{i=1}^{n}{|x_i|^p}\right)^{1/p} \\
where \ p \ge 1 \ be \ a \ real \ number$$
1.2.4 Maximum norm
(special case of:p-norm)
$$\left\|\vec{x}\right\|_\infty:=\max_{i=1}^{n}{|x_i|}$$
1.2.5 Infinite-dimensional case无穷维度情况
无穷维度情况就是将求和相应改成求积分：
例如，有限维度中p-范数为：
$$\left\|\vec{x}\right\|_p:=\left(\sum_{i=1}^{n}{|x_i|^p}\right)^{1/p} \\
where \ p \ge 1 \ be \ a \ real \ number$$
无穷维度中p-范数为：
$$\left\|\vec{x}\right\|_p:=\left(\int_{X}{|x_i|^p} \ dx \right)^{1/p} \\
where \ p \ge 1 \ be \ a \ real \ number$$
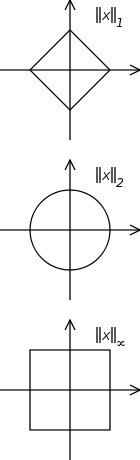上图，当维度为2时，限定l1范数、l2范数、无穷范数的值为1，那么其图形就恰如上图所示。
2 Matrix norm矩阵范数
2.1 Definition定义
In what follows,
$K$
will denote a field of either real or complex numbers.下来，K将表示实数或复数域。
Let
$K^{m \times n}$
denote the vector space of all matrices of size
$m \times n$
(with
$m$
rows and
$n$
columns) with entries in the field
$K$
. 让$K^{m \times n}$表示所有形状为$m \times n$所有矩阵组成的向量空间。
A matrix norm is a norm on the vector space
$K^{m \times n}$
. Thus, the matrix norm is a function
$\left\|\cdot\right\|:K^{m \times n}\rightarrow \mathbb{R}$
that must satisfy the following properties: 矩阵的范数是在向量空间$K^{m \times n}$上的范数。因此，矩阵范数是方程$\left\|\cdot\right\|:K^{m \times n}\rightarrow \mathbb{R}$，方程必须满足如下特性：
For all scalars
$\alpha$
in
$K$
and for all matrices
$\mathbf{A}$
and
$\mathbf{B}$
in
$K^{m \times n}$ :对$K$内的所有标量$\alpha$和$K^{m \times n}$内的$\mathbf{A}$、$\mathbf{B}$：
$\left\|\alpha \mathbf{A}\right\|=|\alpha|\left\|\mathbf{A}\right\|$(being absolutely homogeneous)是绝对齐次的。$\left\|\mathbf{A+B}\right\| \le \left\|\mathbf{A}\right\|+\left\|\mathbf{B}\right\|$(being sub-additive or satisfying the triangle inequality)是次加性的也就是满足三角不等式。$\left\|\mathbf{A}\right\| \ge 0$(being positive-valued)是正值的。$\left\|\mathbf{A}\right\| = 0$iff$\mathbf{A}=\mathbf{0}_{m \times n}$(being definite)$\left\|\mathbf{A}\right\| = 0$当且仅当$\mathbf{A}=\mathbf{0}_{m \times n}$（充要性）
Additionally, in the case of square matrices (thus, m = n), some (but not all) matrix norms satisfy the following condition, which is related to the fact that matrices are more than just vectors:进一步，在方阵情况下（也就是m=n），一些（但不是全部）矩阵范数满足如下条件，因为矩阵不仅仅是向量：
$\left\|\mathbf{AB}\right\| \le \left\|\mathbf{A}\right\|\left\|\mathbf{B}\right\|$for all matrices$\mathbf{A}$and$\mathbf{B}$in$K^{m \times n}$. 对$K^{m \times n}$内的任意矩阵$\mathbf{A}$和$\mathbf{B}$有$\left\|\mathbf{AB}\right\| \le \left\|\mathbf{A}\right\|\left\|\mathbf{B}\right\|$。
A matrix norm that satisfies this additional property is called a sub-multiplicative norm (in some books, the terminology matrix norm is used only for those norms which are sub-multiplicative).满足这一附加性质的矩阵范数称为次乘法范数(在某些书中，术语矩阵范数仅用于那些次乘法范数)。
The definition of sub-multiplicativity is sometimes extended to non-square matrices, for instance in the case of the induced p-norm, where for
$\mathbf{A} \in K^{m \times n}$
and
$\mathbf{B} \in K^{n \times k}$
holds that
$\left\|\mathbf{AB}\right\|_q \le \left\|\mathbf{A}\right\|_p\left\|\mathbf{B}\right\|_q$
. Here
$\left\|\cdot\right\|_p$
and
$\left\|\cdot\right\|_q$
are the norms induced from
$K^n$
and
$K^k$
, respectively, and $p,q \ge 1$. 次乘法性的定义有时可以扩展到非方阵，例如，诱导的p-范数的情况，其中$\mathbf{A} \in K^{m \times n}$并$\mathbf{B} \in K^{n \times k}$，必定有$\left\|\mathbf{AB}\right\|_q \le \left\|\mathbf{A}\right\|_p\left\|\mathbf{B}\right\|_q$，$\left\|\cdot\right\|_p$和$\left\|\cdot\right\|_q$是由$K^n$和$K^k$诱导的范数，当然$p,q \ge 1$。
There are three types of matrix norms which will be discussed below: 有3种类型的矩阵范数：
- Matrix norms induced by vector,由向量范数诱导的矩阵范数；
- Entrywise matrix norms,逐元素的矩阵范数；
- Schatten norms. Schatten范数。
2.2 Matrix norms induced by vector由向量范数诱导的矩阵范数
given a norm
$\left\|\cdot\right\|_{\alpha}$
on
$K^{n}$
, and a norm
$\left\|\cdot\right\|_{\beta}$
on
$K^{m}$
, one can define a matrix norm on
$K^{m\times n}$
induced by these norms: 给定$K^{n}$上的范数$\left\|\cdot\right\|_{\alpha}$和$K^{m}$上的范数$\left\|\cdot\right\|_{\beta}$，可以定义由这两个范数诱导的$K^{m\times n}$上的矩阵范数：
$$\left\|\mathbf{A}\right\|_{\alpha ,\beta }=\max _{\vec{x}\neq \vec{0}}{\frac {\left\|\mathbf{A}\vec{x}\right\|_{\beta }}{\left\|\vec{x}\right\|_{\alpha }}}$$
The matrix norm
$\left\|\mathbf{A}\right\|_{\alpha ,\beta }$
is sometimes called a subordinate norm. Subordinate norms are consistent with the norms that induce them, giving
$\left\|\mathbf{A}\vec{x}\right\|_{\beta }\leq \left\|\mathbf{A}\right\|_{\alpha ,\beta }\left\|\vec{x}\right\|_{\alpha }$. 矩阵范数$\left\|\mathbf{A}\right\|_{\alpha ,\beta }$有时被称为从属范数。从属范数与诱导它们的范数是一致的，有$\left\|\mathbf{A}\vec{x}\right\|_{\beta }\leq \left\|\mathbf{A}\right\|_{\alpha ,\beta }\left\|\vec{x}\right\|_{\alpha }$。
Any induced operator norm is a sub-multiplicative matrix norm:
$\left\|\mathbf{AB}\right\|\leq \left\|\mathbf{A}\right\|\left\|\mathbf{B}\right\|$
; this follows from
$\left\|\mathbf{AB}\vec{x}\right\|\leq \left\|\mathbf{A}\right\|\left\|\mathbf{B}\vec{x}\right\|\leq \left\|\mathbf{A}\right\|\left\|\mathbf{B}\right\|\left\|\vec{x}\right\|$
and
$\max \limits _{\left\|\vec{x}\right\|=1}\left\|\mathbf{AB}\vec{x}\right\|=\left\|\mathbf{AB}\right\|$.任何诱导的操作范数是次加性矩阵范数：$\left\|\mathbf{AB}\right\|\leq \left\|\mathbf{A}\right\|\left\|\mathbf{B}\right\|$；因为$\left\|\mathbf{AB}\vec{x}\right\|\leq \left\|\mathbf{A}\right\|\left\|\mathbf{B}\vec{x}\right\|\leq \left\|\mathbf{A}\right\|\left\|\mathbf{B}\right\|\left\|\vec{x}\right\|$和$\max \limits _{\left\|\vec{x}\right\|=1}\left\|\mathbf{AB}\vec{x}\right\|=\left\|\mathbf{AB}\right\|$。
Moreover, any induced norm satisfies the inequality
$\left\|\mathbf{A}^{r}\right\|^{1/r}\geq \rho (\mathbf{A}) \tag{1}$,
where $\rho(\mathbf{A})$ is the spectral radius of \mathbf{A}. For symmetric or hermitian $\mathbf{A}$, we have equality in (1) for the 2-norm, since in this case the 2-norm is precisely the spectral radius of $\mathbf{A}$. For an arbitrary matrix, we may not have equality for any norm; a counterexample being given by
$\mathbf{A}={\begin{bmatrix}0&1\\0&0\end{bmatrix}}$
, which has vanishing spectral radius. In any case, for square matrices we have the spectral radius formula:
$\lim _{r\rightarrow \infty }\left\|A^{r}\right\|^{1/r}=\rho (A)$. 而且，任何诱导范数满足不等式$\left\|A^{r}\right\|^{1/r}\geq \rho (A) \tag{1}$，其中$\rho(\mathbf{A})$是$\mathbf{A}$的谱半径。对于对称或厄密矩阵$\mathbf{A}$，我们在(1)中对于2-范数是相等的，因为在这种情况下2-范数恰好是$\mathbf{A}$的谱半径。对于其他任意矩阵的任意范数(1)式很可能不能取等号；可以举反例$\mathbf{A}={\begin{bmatrix}0&1\\0&0\end{bmatrix}}$，其有消失的谱半径。无论如何，对方阵有谱半径公式：$\lim _{r\rightarrow \infty }\left\|\mathbf{A}^{r}\right\|^{1/r}=\rho (\mathbf{A})$。
2.2.1 Special cases特例
$$\left\|\mathbf{A}\right\|_1=\max_{1 \le j \le n}{\sum_{i=1}^{m}{|a_{ij}|}}$$
即先对元素的绝对值按列求和后再挑最大的。
$$\left\|\mathbf{A}\right\|_\infty=\max_{1 \le i \le m}{\sum_{j=1}^{n}{|a_{ij}|}}$$
即先对元素的绝对值按行求和后再挑最大的。
$$\left\|\mathbf{A}\right\|_2=\sigma_{max}(\mathbf{A}) =\sqrt{\lambda_{max}(\mathbf{A^*A})} \le \left(\sum_{i=1}^{m}{\sum_{j=1}^{n}{|a_{ij}|^2}}\right)^{1/2}=\left\|\mathbf{A}\right\|_F$$
$\sigma_{max}(\mathbf{A})$是矩阵$\mathbf{A}$最大的奇异值，$\mathbf{A^*}$是$\mathbf{A}$的共轭转置（对于复数组成的矩阵才需要共轭），$\left\|\mathbf{A}\right\|_F$是Frobenius范数。
2.3 Entrywise matrix norms逐元素的矩阵范数
$L_{p,q}$norm, $p, q \ge 1$, defined by:范数$L_{p,q}$（$p, q \ge 1$）定义如下：
$$\left\| \mathbf{A}\right\| _{p,q}=\left(\sum _{j=1}^{n}\left(\sum _{i=1}^{m}|a_{ij}|^{p}\right)^{q/p}\right)^{1/q}$$
$L_{p,p}$可直接记作$L_{p}$。
2.3.1 Frobenius norm Frobenius范数
When $p = q = 2$ for the
$L_{p,q}$
norm, it is called the Frobenius norm or the Hilbert–Schmidt norm, though the latter term is used more frequently in the context of operators on (possibly infinite-dimensional) Hilbert space. This norm can be defined in various ways:
$\left\|\mathbf{A}\right\|_{\rm {F}}={\sqrt {\sum _{i=1}^{m}\sum _{j=1}^{n}|a_{ij}|^{2}}}={\sqrt {\operatorname {trace} \left(\mathbf{A^{*}A}\right)}}={\sqrt {\sum _{i=1}^{\min\{m,n\}}\sigma _{i}^{2}(\mathbf{A})}}$.
where
$\sigma _{i}(\mathbf{A})$
are the singular values of
$\mathbf{A}$
. Recall that the trace function returns the sum of diagonal entries of a square matrix.当$p = q = 2$时，$L_{p,q}$范数叫做Frobenius范数也叫Hilbert–Schmidt范数，后者更常用于Hilbert空间的操作的概念中。Frobenius范数定义为：$\left\|\mathbf{A}\right\|_{\rm {F}}={\sqrt {\sum _{i=1}^{m}\sum _{j=1}^{n}|a_{ij}|^{2}}}={\sqrt {\operatorname {trace} \left(\mathbf{A^{*}A}\right)}}={\sqrt {\sum _{i=1}^{\min\{m,n\}}\sigma _{i}^{2}(\mathbf{A})}}$。其中$\sigma _{i}(\mathbf{A})$是$\mathbf{A}$的奇异值。回想一下trace函数返回的是方阵对角线元素的和。
The Frobenius norm is the Euclidean norm on
$K^{n\times n}$
and comes from the Frobenius inner product on the space of all matrices. Frobenius范数是$K^{n\times n}$上的欧式范数并且来自$K^{n\times n}$上所有矩阵的Frobenius内积。
The Frobenius norm is sub-multiplicative and is very useful for numerical linear algebra. This norm is often easier to compute than induced norms and has the useful property of being invariant under rotations, that is,
$\left\|\mathbf{A}\right\|_{\rm {F}}^{2}=\left\|\mathbf{AR}\right\|_{\rm {F}}^{2}=\left\|\mathbf{RA}\right\|_{\rm {F}}^{2}$
for any rotation matrix
$\mathbf{R}$
. This property follows from the trace definition restricted to real matrices:
$\left\|\mathbf{AR}\right\|_{\rm {F}}^{2}=\operatorname {trace} \left(\mathbf{R}^{\textsf {T}}\mathbf{A}^{\textsf {T}}\mathbf{AR}\right)=\operatorname {trace} \left(\mathbf{RR}^{\textsf {T}}\mathbf{A}^{\textsf {T}}\mathbf{A}\right)=\operatorname {trace} \left(\mathbf{A}^{\textsf {T}}\mathbf{A}\right)=\left\|\mathbf{A}\right\|_{\rm {F}}^{2}$
and
$\left\|\mathbf{RA}\right\|_{\rm {F}}^{2}=\operatorname {trace} \left(\mathbf{A}^{\textsf {T}}\mathbf{R}^{\textsf {T}}\mathbf{R}\mathbf{A}\right)=\operatorname {trace} \left(\mathbf{A}^{\textsf {T}}\mathbf{A}\right)=\left\|\mathbf{A}\right\|_{\rm {F}}^{2}$,
where we have used the orthogonal nature of
$\mathbf{R}$
(that is,
$\mathbf{R}^{\textsf {T}}\mathbf{R}=\mathbf{RR}^{\textsf {T}}=\mathbf {\mathbf{I}}$
) and the cyclic nature of the trace (
$\operatorname {trace} (\mathbf{XYZ})=\operatorname {trace} (\mathbf{ZXY})$
). More generally the norm is invariant under a unitary transformation for complex matrices. Frobenius范数是次加性的并对数字线性代数很有用。这个模量比诱导模量更易计算并有旋转下不变这一有用特性，也就是，对于任何旋转矩阵$\mathbf{R}$有$\left\|\mathbf{A}\right\|_{\rm {F}}^{2}=\left\|\mathbf{AR}\right\|_{\rm {F}}^{2}=\left\|\mathbf{RA}\right\|_{\rm {F}}^{2}$。这一特性的根据是严格的实数矩阵的迹的定义：$\left\|\mathbf{AR}\right\|_{\rm {F}}^{2}=\operatorname {trace} \left(\mathbf{R}^{\textsf {T}}\mathbf{A}^{\textsf {T}}\mathbf{AR}\right)=\operatorname {trace} \left(\mathbf{RR}^{\textsf {T}}\mathbf{A}^{\textsf {T}}\mathbf{A}\right)=\operatorname {trace} \left(\mathbf{A}^{\textsf {T}}\mathbf{A}\right)=\left\|\mathbf{A}\right\|_{\rm {F}}^{2}$和$\left\|\mathbf{RA}\right\|_{\rm {F}}^{2}=\operatorname {trace} \left(\mathbf{A}^{\textsf {T}}\mathbf{R}^{\textsf {T}}\mathbf{R}\mathbf{A}\right)=\operatorname {trace} \left(\mathbf{A}^{\textsf {T}}\mathbf{A}\right)=\left\|\mathbf{A}\right\|_{\rm {F}}^{2}$，这里我们用到了$\mathbf{R}$的正交本质（也就是$\mathbf{R}^{\textsf {T}}\mathbf{R}=\mathbf{RR}^{\textsf {T}}=\mathbf {\mathbf{I}}$）和迹的环本质（$\operatorname {trace} (\mathbf{XYZ})=\operatorname {trace} (\mathbf{ZXY})$）。更一般地，范数在复矩阵的酉变换下是不变的。
It also satisfies
$\left\|\mathbf{A}^{\rm {T}}\mathbf{A}\right\|_{\rm {F}}=\left\|\mathbf{AA}^{\rm {T}}\right\|_{\rm {F}}\leq \left\|\mathbf{A}\right\|_{\rm {F}}^{2}$
and
$\left\|\mathbf{A+B}\right\|_{\rm {F}}^{2}=\left\|\mathbf{A}\right\|_{\rm {F}}^{2}+\left\|\mathbf{B}\right\|_{\rm {F}}^{2}+2\langle \mathbf{A,B}\rangle _{\mathrm {F} }$,
where
$\langle \mathbf{A,B}\rangle _{\mathrm {F} }$
is the Frobenius inner product. 也满足$\left\|\mathbf{A}^{\rm {T}}\mathbf{A}\right\|_{\rm {F}}=\left\|\mathbf{AA}^{\rm {T}}\right\|_{\rm {F}}\leq \left\|\mathbf{A}\right\|_{\rm {F}}^{2}$和$\left\|\mathbf{A+B}\right\|_{\rm {F}}^{2}=\left\|\mathbf{A}\right\|_{\rm {F}}^{2}+\left\|\mathbf{B}\right\|_{\rm {F}}^{2}+2\langle \mathbf{A,B}\rangle _{\mathrm {F} }$，其中$\langle \mathbf{A,B}\rangle _{\mathrm {F} }$是Frobenius内积。
2.3.2 max norm 最大范数
The max norm is the elementwise norm with $p = q = \infty$:
$\left\|\mathbf{A}\right\|_{\max }=\max _{ij}|a_{ij}|$. 最大范数是$p = q = \infty$的逐元素范数： $\left\|\mathbf{A}\right\|_{\max }=\max _{ij}|a_{ij}|$。
This norm is not sub-multiplicative.这一范数不是次加性的。
2.4 Schatten norms Schatten范数
The Schatten p-norms arise when applying the p-norm to the vector of singular values of a matrix. If the singular values are denoted by $\sigma_i$, then the Schatten p-norm is defined by
$\left\|\mathbf{A}\right\|_{p}=\left(\sum _{i=1}^{\min\{m,\,n\}}\sigma _{i}^{p}(\mathbf{A})\right)^{1/p}$. 当将p范数应用于矩阵奇异值向量时，产生了Schatten p范数。如果奇异值表示为$\sigma_i$，那么Schatten p范数定义为$\left\|\mathbf{A}\right\|_{p}=\left(\sum _{i=1}^{\min\{m,\,n\}}\sigma _{i}^{p}(\mathbf{A})\right)^{1/p}$。
These norms again share the notation with the induced and entrywise p-norms, but they are different. Schatten p范数与逐元素p范数标注相同，但两者是不同的。
All Schatten norms are sub-multiplicative. They are also unitarily invariant, which means that
$\left\|\mathbf{A}\right\|=\left\|\mathbf{UAV}\right\|$
for all matrices
$\mathbf{A}$
and all unitary matrices
$\mathbf{U}$
and
$\mathbf{V}$
. 所有Schatten p范数都是次加性的，它们也是一致不变量，也就是说对所有矩阵$\mathbf{A}$、所有一致矩阵$\mathbf{U}$和$\mathbf{V}$有$\left\|\mathbf{A}\right\|=\left\|\mathbf{UAV}\right\|$。
The most familiar cases are $p = 1，2 \infty$. The case $p = 2$ yields the Frobenius norm, introduced before. The case $p = \infty$ yields the spectral norm, which is the operator norm induced by the vector 2-norm (see above). Finally, $p = 1$ yields the nuclear norm (also known as the trace norm, or the Ky Fan 'n'-norm[3]), defined as
$\left\|\mathbf{A}\right\|_{*}=\operatorname {trace} \left({\sqrt {\mathbf{A^{*}A}}}\right)=\sum _{i=1}^{\min\{m,\,n\}}\!\sigma _{i}(\mathbf{A})$.
(Here
${\sqrt {\mathbf{A^{*}A}}}$
denotes a positive semidefinite matrix
$\mathbf{B}$
such that
$\mathbf{BB}=\mathbf{A^{*}A}$
. More precisely, since
$\mathbf{A^{*}A}$
is a positive semidefinite matrix, its square root is well-defined.) 最熟悉的案例是$p = 1，2 \infty$。当$p = 2$就是Frobenius范数。当$p = \infty$就是谱范数，也就是向量2范数诱导的操作范数。当$p = \infty$就是Frobenius范数。当$p = 1$就是核范数（也叫迹范数、Ky Fan 'n'-范数），定义为$\left\|\mathbf{A}\right\|_{*}=\operatorname {trace} \left({\sqrt {\mathbf{A^{*}A}}}\right)=\sum _{i=1}^{\min\{m,\,n\}}\!\sigma _{i}(\mathbf{A})$。（这里${\sqrt {\mathbf{A^{*}A}}}$表示半正定矩阵$\mathbf{B}$使得$\mathbf{BB}=\mathbf{A^{*}A}$。或者更精确地，既然$\mathbf{A^{*}A}$是半正定矩阵，那么其平方根是存在定义的。）
参考：