逻辑回归logistic_regression
1 回归(Regression)
回归，我的理解来说，其直观的理解就是拟合的意思。我们以线性回归为例子，在二维平面上有一系列红色的点，我们想用一条直线来尽量拟合这些红色的点，这就是线性回归。回归的本质就是我们的预测结果尽量贴近实际观测的结果，或者说我们的求得一些参数，经过计算之后的预测结果尽可能接近真实值。
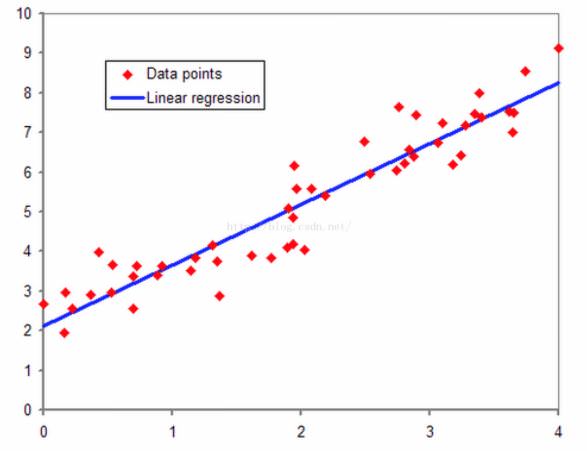按照机器学习的一些作者的叙述，如果目标变量是连续型的，那么是回归；如果预测变量是离散型的，那么是分类。
最简单的回归是普通最小二乘法回归（Ordinary Least Squares），在sklearn中是sklearn.linear_model.LinearRegression。数学上即解决以下数学问题。
$$\min_{w} {|| \mathbf{X} \vec{w} - \vec{y}||_2}^2$$
也就是损失函数为MSE。
2 逻辑回归的由来
对于二类线性可分的数据集，使用线性感知器就可以很好的分类。如下图中红色和蓝色的点，我们使用一条直线$x_1 +x_2 = 3$就可以区分两种数据集，在直线上方的属于红色类，直线下方的属于蓝色类。
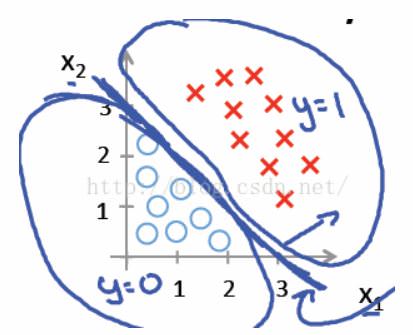线性回归和非线性回归的分类问题都不能给予解答，因为线性回归和非线性回归的问题，假设其分类函数如下：
$$y=\vec{w}^T\vec{x}+b$$
这里$\vec{x}$是数据矩阵$\mathbf{X}$中的一行。
但是如果我们想知道对于一个二类分类问题，对于具体的一个样例，我们不仅想知道该类属于某一类，而且还想知道该类属于某一类的概率多大,有什么办法呢？
y的阈值处于$(-\infty，+\infty)$，此时不能很好的给出属于某一类的概率，因为概率的范围是$(0,1)$，我们需要一个更好的映射函数，能够将分类的结果很好的映射成为$(0,1)$之间的概率，并且这个函数能够具有很好的可微分性。在这种需求下，人们找到了这个映射函数，即逻辑斯谛函数，也就是我们常说的sigmoid函数，其形式如下：
$$\frac{1}{1+e^{-z}}$$
sigmoid函数图像如下图所示
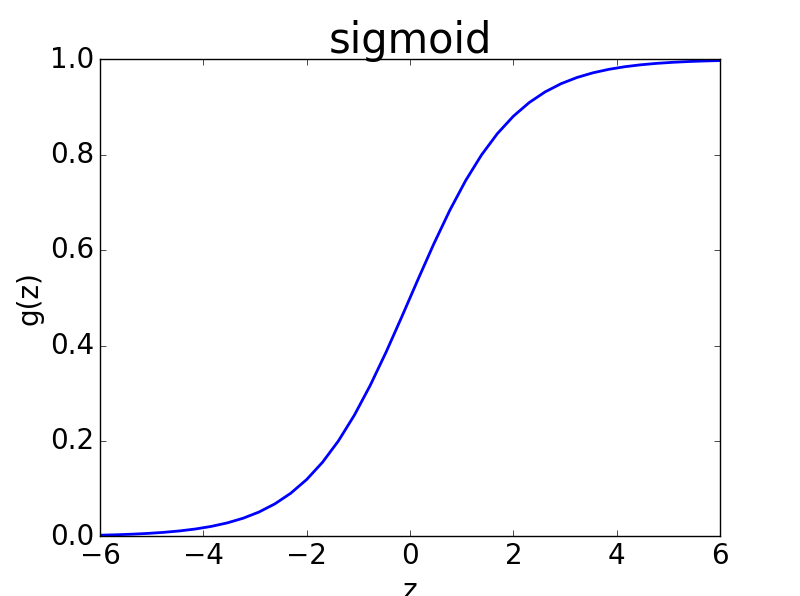如图，其可以将$(-\infty，+\infty)$数据映射到$(0,1)$，正好满足我们的要求。
sigmoid函数完美的解决了上述需求，而且sigmoid函数连续可微分。 假设数据离散二类可分，分为0类和1类,如果概率值大于1/2，我们就将该类划分为1类，如果概率值低于1/2,我们就将该类划分为0类。当z取值为0的时候，概率值为1/2，这时候需要人为规定划分为哪一类。
但是如果二类线性不可分的数据集，我们无法找到一条直线能够将两种类别很好的区分，即线性回归的分类法对于线性不可分的数据无法有效分类。例如下图中的红色点和蓝色点，我们无法使用一条直线很好的区分这两类，但是我们可以使用非线性分类器，如果我们使用${x_1}^2+{x_2}^2 = 1$，在圆外面的为红色类，在圆里面的一类为蓝色类。
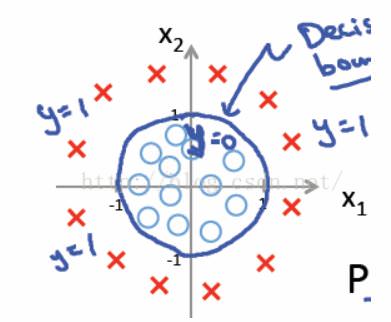诚然，数据线性可分可以使用线性分类器，如果数据线性不可分，可以使用非线性分类器，然后再运用sigmoid函数，这样就是非线性逻辑回归。
但以下讨论仅限于线性可分的情况的逻辑回归。
3 为什么采用sigmoid函数
http://www.win-vector.com/dfiles/LogisticRegressionMaxEnt.pdf
3 逻辑回归的损失函数(Loss Function)和成本函数(Cost Function)
在二类分类中，我们假定sigmoid输出结果表示属于1类的概率值，我们很容易想到用平方损失函数（也就是MSE），即
$$J(\vec{w})=\sum_{i=1}^{n}{\frac{1}{2}(\hat{y}_{i}-y_{i})^2}=\sum_{i=1}^{n}{\frac{1}{2}(\phi({z}_i)-y_{i})^2}=\sum_{i=1}^{n}{\frac{1}{2}(\phi(\vec{w}^T\vec{x}_i+b)-y_{i})^2}$$
这里$z_i=\vec{w}^T\vec{x}_i+b$，$i$代表第$i$个样本点。$\hat{y}_i$代表第$i$个样本的预测值，$y_i$代表第$i$个样本的实际值，$\phi{(z_i)}$代表对第$i$个$z$施加sigmoid函数。
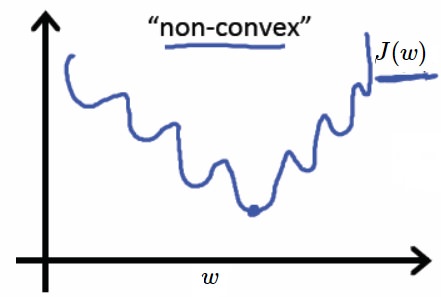
在这种情况下，我们$\phi({z_{i}})$表示sigmoid对第i个值的预测结果，我们将sigmoid函数带入上述成本函数中，绘制其图像，发现这个成本函数的函数图像是一个非凸函数，如下图所示，这个函数里面有很多极小值，如果采用梯度下降法，则会导致陷入局部最优解中,有没有一个凸函数的成本函数呢？
Cross entropy can be used to define a loss function in machine learning and optimization. The true probability
$p_{i}$
is the true label, and the given distribution
$q_{i}$
is the predicted value of the current model.交叉熵可以用来定义机器学习和优化中的损失函数。真实概率$p_{i}$是真实的标签，给定的分布$q_{i}$是当前模型的预测值。
More specifically, let us consider logistic regression, which (in its most basic form) deals with classifying a given set of data points into two possible classes generically labelled
$0$
and
$1$
. The logistic regression model thus predicts an output
$y\in \{0,1\}$
, given an input vector
$\vec {x}$
. The probability is modeled using the logistic function
$g(z)=1/(1+e^{-z})$
. Namely, the probability of finding the output
$y=1$
is given by:更具体地说，让我们考虑逻辑回归，它(以其最基本的形式)处理将给定的一组数据点分类为通常标记为$0$和$1$的两个可能的类。因此，逻辑回归模型预测给定输入向量$\vec {x}$的输出$y\in \{0,1\}$。概率是用逻辑函数$g(z)=1/(1+e^{-z})$建模的。即，得到输出$y=1$的概率为：
$$q_{y=1}\ =\ {\hat {y}}\ \equiv \ g(\vec {w}^T \cdot \vec {x} +b)\ =1/(1+e^{-(\vec {w}^T \cdot \vec {x} +b)})$$
where the vector of weights
$\mathbf {w}$
is optimized through some appropriate algorithm such as gradient descent. Similarly, the complementary probability of finding the output
$y=0$
is simply given by:其中权向量$\mathbf {w}$通过梯度下降等适当算法进行优化。类似地，输出$y=0$的互补概率简单地由以下方程给出：
$$q_{y=0}\ =\ 1-{\hat {y}}\equiv \ 1-g(\vec {w}^T \cdot \vec {x} +b)\ =1-1/(1+e^{-(\vec {w}^T \cdot \vec {x} +b)})$$
The true (observed) probabilities can be expressed similarly as
$p_{y=1}=y$
and
$p_{y=0}=1-y$
.真实(观测)概率可以类似地表示为$p_{y=1}=y$和$p_{y=0}=1-y$。
Having set up our notation,
$p \in \{y,1-y\}$
and
$q \in \{\hat {y},1-\hat {y}\}$
, we can use cross entropy to get a measure of dissimilarity between
$p$
and
$q$
:设置符号$p \in \{y,1-y\}$和$q \in \{\hat {y},1-\hat {y}\}$，我们可以利用交叉熵来衡量$p$和$q$之间的不同:
$$H(p_i,q_i)\ =-\sum_{i}p_{i}\log q_{i}\ =-y\log{\hat {y}}-(1-y)\log(1-\hat{y})$$
The typical cost function that one uses in logistic regression is computed by taking the average of all cross-entropies in the sample. For example, suppose we have
$n$
samples with each sample indexed by
$i=1,\dots ,n$
. The loss function is then given by:在逻辑回归中使用的典型成本函数是通过取样本中所有交叉熵的平均值来计算的。例如，假设我们有$n$个样本，每个样本的索引为$i=1,\dots ,n$。则损失函数为:
$${\begin{aligned}J(\vec {w},b )\ &=\ {\frac {1}{n}}\sum _{i=1}^{n}H(p_{i},q_{i})\ =\ -{\frac {1}{n}}\sum _{i=1}^{n}\ {\bigg [}y_{i}\log {\hat {y}}_{i}+(1-y_{i})\log(1-{\hat {y}}_{i}){\bigg ]}\,,\end{aligned}}$$
where
${\hat {y}}_{i}\equiv g(\vec {w}^T \cdot \vec {x} _{i}+b)=1/(1+e^{-(\vec {w}^T \cdot \vec {x} +b)})$
, with
$g(z)$
the logistic function as before.其中${\hat {y}}_{i}\equiv g(\vec {w}^T \cdot \vec {x} _{i}+b)=1/(1+e^{-(\vec {w}^T \cdot \vec {x} +b)})$，其中逻辑函数$g(z)$如前所述。
The logistic loss is sometimes called cross-entropy loss. It is also known as $\log$ loss (In this case, the binary label is often denoted by {-1,+1}).逻辑损失有时称为交叉熵损失。它也称为$\log$损失（在这种情况下，二分类标签通常表示为{-1,+1}）。
这是一个凸函数（斜率是非单调递减的函数即凸函数），因此可以用梯度下降法求其最小值。
4 极大似然法求解逻辑回归
还可以用我们熟知的统计学知识——极大似然法估计逻辑回归中的参数$\vec{x}$和$b$，上述得到的$\log{p(y|\vec{w},\vec{x})}$,假设目前有n组样本，分别为$(\vec{x}_1,y_1),(\vec{x}_2,y_2),\ldots,(\vec{x}_n,y_n)$，其中$\vec{x}_1$表示第i个样本的特征，$y_i$表示第i个样本的类别，$y_i=0$或者$y_i=1$，
假设sigmoid函数$\phi{(z_i)}$表示属于1类的概率，于是做出如下的定义：
$$\left\{ \begin{aligned} p(y_i=1|\vec{x}_i) & = \phi{(\vec{w}^T \cdot \vec{x}_i +b)}=\phi{(z_i)} \\ p(y_i=0|\vec{x}_i) & = 1-\phi{(z_i)} \end{aligned} \right.$$
将两个式子综合来，可以改写为下式：
$$p(y_i|\vec{x}_i) = {\hat{y}_i}^{y_i}{(1-\hat{y}_i)}^{(1-y_i)}$$
因为$y_i \in \{0,1\}$；当$y_i=0$时，上式退化为$p(y_i|\vec{x}_i) = {(1-\hat{y}_i)}$；当$y_i=1$时，上式退化为$p(y_i|\vec{x}_i) = {\hat{y}_i}$。
利用极大似然法的原则，假设所有训练样本独立同分布，则联合概率为所有样本概率的乘积，即：
$$P(\vec{y})=\prod_{i=1}^{n}{P(y_i|\vec{x}_i)}$$
对上述公式两边取对数，得到下述公式，是不是对这个公式优点熟悉呢？这个公式就是我们的成本函数的和，对于这个公式和成本函数来说，取平均值和不取平均值没有影响。
$$\log{P(\vec{y})}=\log{\prod_{i=1}^{n}{P(y_i|\vec{x}_i)}}=\sum_{i=1}^{n}{\log{P(y_i|\vec{x}_i)}}=\sum_{i=1}^{n}{H(p_i,q_i)}$$
按照极大似然法求极值的方法，分别对$\vec{w}$的每个参数求偏导数使其为0，得到对数似然方程组，求解该方程，便可以到的$\vec{w}$的参数。只是如果参数很多，求解方程组就会很复杂，此时可以考虑梯度下降法来求解。
由上面叙述，交叉熵损失函数与极大似然法是等效的。
5 总结
- 逻辑回归最大的优势在于它的输出结果不仅可以用于分类，还可以表征某个样本属于某类别的概率。
- 逻辑斯谛函数将原本输出结果从范围
$(-\infty，+\infty)$映射到$(0,1)$，从而完成概率的估测。 - 逻辑回归得判定的阈值能够映射为平面的一条判定边界，随着特征的复杂化，判定边界可能是多种多样的样貌，但是它能够较好地把两类样本点分隔开，解决分类问题。
- 求解逻辑回归参数的传统方法是梯度下降，构造为凸函数的代价函数后，每次沿着偏导方向(下降速度最快方向)迈进一小部分，直至N次迭代后到达最低点。
- 查阅sklearn文档
sklearn.linear_model.LogisticRegression发现其并没有损失函数的选择，言外之意其损失函数是固定的，也就是损失函数固定为交叉熵。这是普通最小二乘法线性回归与普通逻辑回归最重要的区别。
参考：