Kaggle之Store item demand forecasting challenge竞赛项目总结
1.项目情况
kaggle的Store Item Demand Forecasting Challenge竞赛,
有2013年初到2017年末10个商店、50种货物每日销量情况,预测2018年头3个月这些商店、货物的每日销售情况。竞赛要求结果采用SMAPE度量。
$$SMAPE=100 \text{%} \frac{1}{n} \sum_{i=1}^{n} \frac{|A_i-F_i|}{(|A_i|+|F_i|)/2}$$
$A_i$代表第i个样本的真实值,$F_i$代表第i个样本的预测值。
2.项目成绩
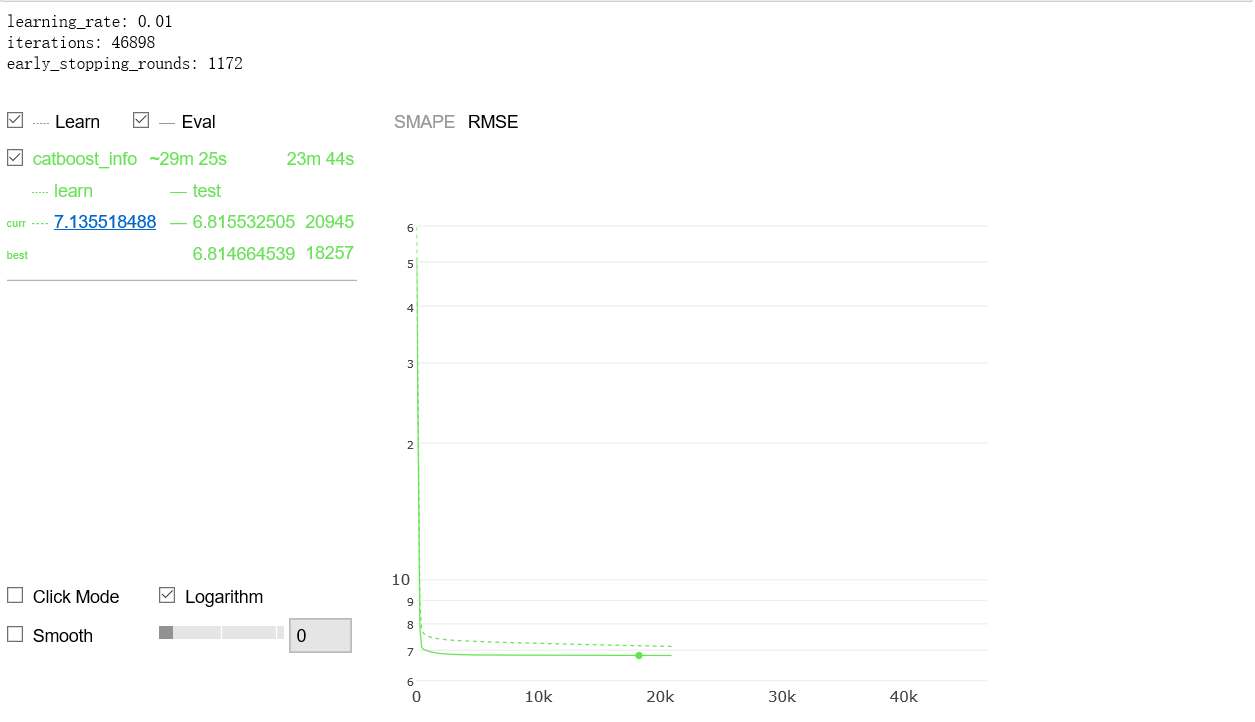
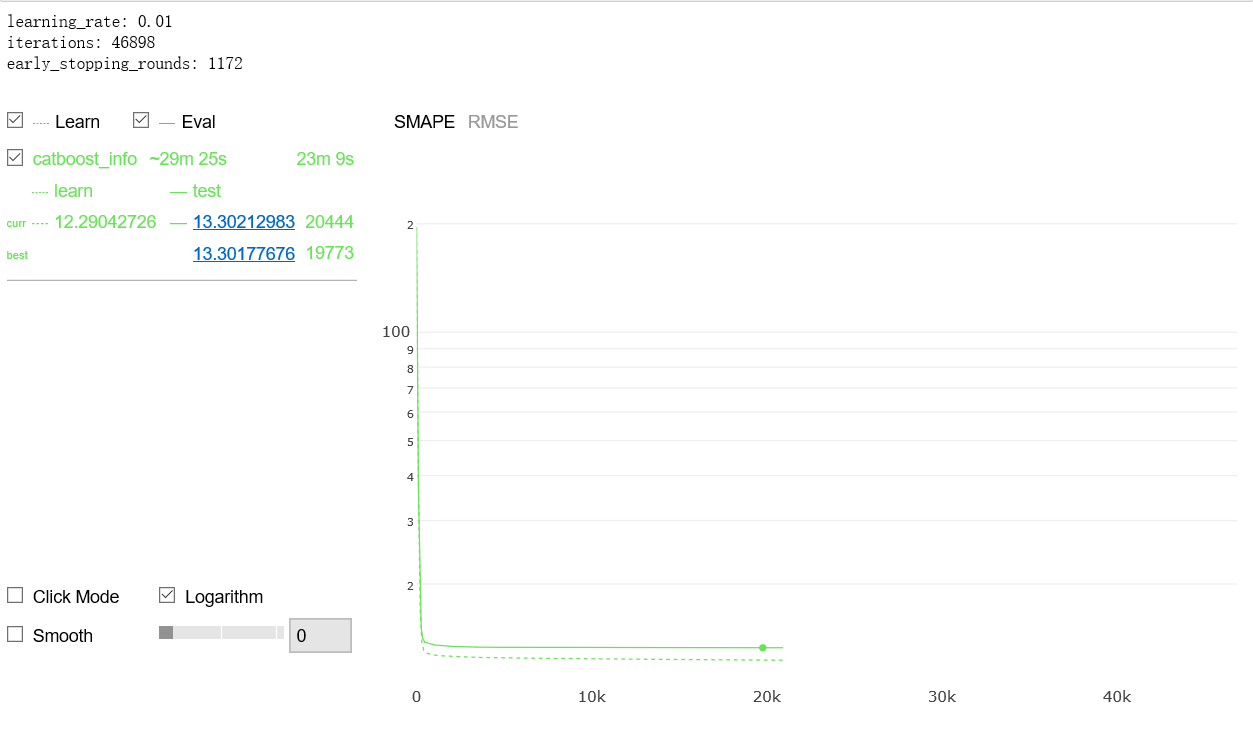
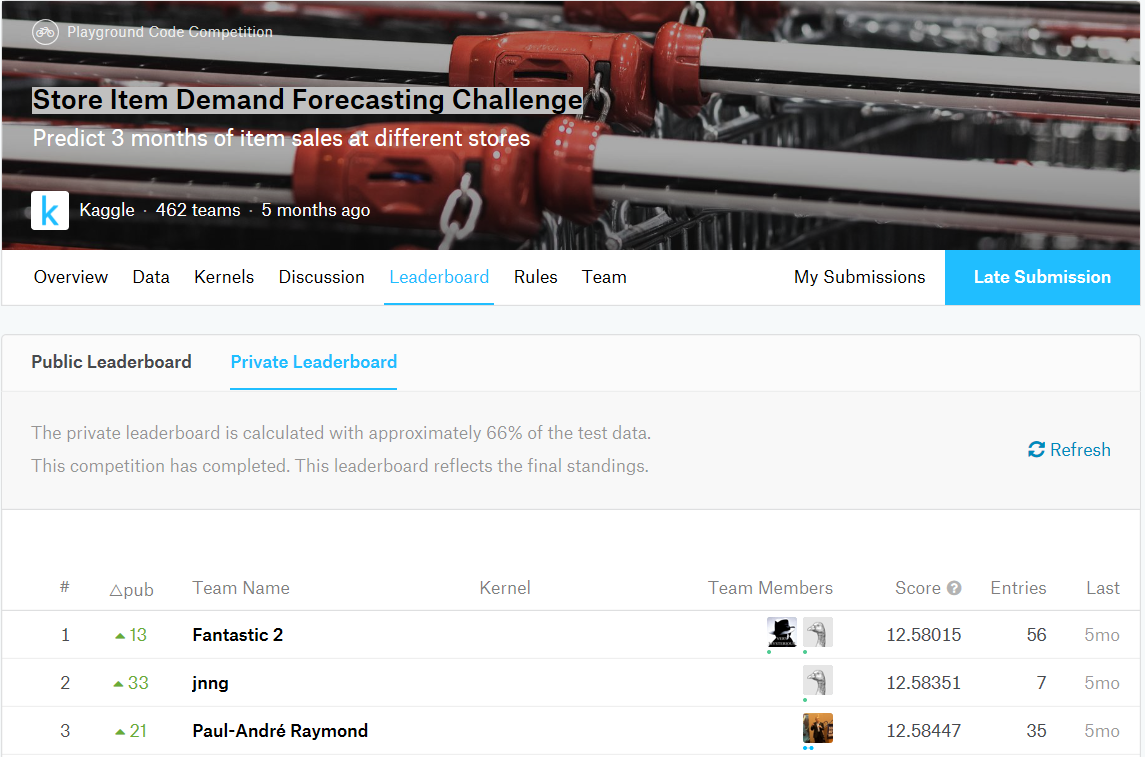
以下代码采用2014年、2015年和2016年数据用于训练,2017年数据用于验证,模型采用损失函数RMSE,度量函数SMAPE。得到训练smape约12.30[11],2017年smape为11.860766606767626[12],2014年第一季度smape为14.645917711865364[3],2015年第一季度smape为14.091883155407277[4],2016年第一季度smape为13.476791353148277[5],2017年第一季度smape为13.301776762020786[6]。据此推断2018年第一季度smape约12.5846141148,与竞赛最优成绩12.58015相当,可惜不在竞赛时段,无法最终验证。依据如下:
损失函数采用RMSE,
$$RMSE=\sqrt{\frac{1}{n} \sum_{i=1}^{n} {(A_i-F_i)}^{2}}$$
其关注的是绝对误差,而且RMSE对绝对误差的离散程度容忍较小,个体绝对误差偏离均值将显著增加RMSE,因此RMSE倾向于减小绝对误差并使绝对误差尽可能均一化。
模型的绝对误差接近均一化,但是由于实际销量情况随时间是不平衡的,这就是造成smape差异的原因。
为估计2018年第一季度smape,作如下假设:
- SMAPE约等于销量绝对误差的平均值除以销量的平均值。即:
$$SMAPE=\frac{1}{n} \sum_{i=1}^{n} \frac{|A_i-F_i|}{(|A_i|+|F_i|)/2} \approx \frac{\frac{1}{n} \sum_{i=1}^{n} |A_i-F_i|}{\frac{1}{n} \sum_{i=1}^{n} (|A_i|+|F_i|)/2} \approx \frac{\frac{1}{n} \sum_{i=1}^{n} |A_i-F_i|}{\frac{1}{n} \sum_{i=1}^{n} |A_i|}$$ - 2018年第一季度销量平均值取自2013年第一季度、2014年第一季度、2015年第一季度、2016年第一季度、2017年第一季度销量平均值的最小二乘法线性插值。
smape计算
| 时间 | 平均绝对误差[8] | 平均销量[9] | smape |
|---|---|---|---|
| 2014q1 | 572.6247872118 | 39.097911[1] | 14.645917711865364[3] |
| 2015q1 | 574.5670977178 | 40.772911[1] | 14.091883155407277[4] |
| 2016q1 | 594.8380237664 | 44.137956[1] | 13.476791353148277[5] |
| 2017q1 | 609.3224692039 | 45.807600[1] | 13.301776762020786[6] |
| 2018q1 | 620.8601[7] | 49.334854[2] | 12.5846141148 |
备注:
- 2014q1、2015q1、2016q1和2017q1的平均销量见Out[26]。
- 2018q1的平均销量取自2013q1到2017q1平均销量的最小二乘法线性插值。
- 2014q1的smape见Out[92]。
- 2015q1的smape见Out[93]。
- 2016q1的smape见Out[94]。
- 2017q1的smape见Out[90]。
- 2018q1的平均绝对误差取自2014q1到2017q1平均绝对误差的最小二乘法线性插值。
- 平均绝对误差即
$\frac{1}{n} \sum_{i=1}^{n} |A_i-F_i|$。 - 平均销量即
$\frac{1}{n} \sum_{i=1}^{n} |A_i|$。 - 最小二乘法线性回归公式
$y=ax+b$、$a = \frac{n\sum_{i=1}^{n}xy - \sum_{i=1}^{n}x\sum_{i=1}^{n}y}{n\sum_{i=1}^{n}x^2 - {(\sum_{i=1}^{n}x)}^2}$、$b=\hat{y}-a\hat{x}$。 - 2014-2016年的smape见Out[89]。
- 2017年的smape见Out[91]。
竞赛排行耪: https://www.kaggle.com/c/demand-forecasting-kernels-only/leaderboard,名称feiyang0chen1
3.项目心得体会:
- 防止泄露是关键。时间序列的预测不可避免要利用需要预测的目标值本身构造特征。竞赛历史数据时间段为2013.1.1~2017.12.31,需要预测2018.1.1~2018.3.31时间段(90天)10个商店每个商店50种货物销量,那么在利用销量构造特征时必须滞后90天及以上,若含有滞后小于90天的特征,将造成模型训练时效果很好而预测时候效果很差,因为2018.1.1及以后销量没有数据。我构造的特征如果利用了往期销量,要么滞后不小于90,要么分出数据用来作统计构造特征而不参与训练,这样保证了不存在泄露。
- 很自然会想到2018年全年作为验证数据集,建立的模型很容易得到2018年的smape接近12.0,那么据此认为2018年第一季度的smape为12.0吗?不是的,作图可知销量随时间上是不均衡的,事实上年初和年末属于销量淡季,其smape显著大于年中及年平均。
- 多次尝试建立模型发现,模型很容易模拟销量的平均变化,就犹如将往期销量数据平滑了一般,但这就造成了模型很难模拟销量极值出现的情况。特别地,小销量如果出现极小值而模型未抓取,将显著增加模型smape。关键是抓取极值信息,所以我采用2013年销量数据计算了月、日、商店、商品(年中第几周、星期几、商店、商品)联合对应销量的窗口平均与实际销量的差值除以销量(记作mpe)将这个数据的极大值和极小值对应的月、日、商店、商品(年中第几周、星期几、商店、商品)联合分别标记为1,-1,其它月、日、商店、商品(年中第几周、星期几、商店、商品)标记为0,这样构成了一些新的特征。若采用全部历史数据构造这些特征将造成严重泄露,这也从侧面验证了这些数据的有效性。(见In[51~58])
- 同时还发现,月、日、商店、商品(年中第几周、星期几、商店、商品)联合对应销量的窗口平均与实际销量的差值除以销量(记作mpe)本身对模型是没有贡献的,因为mpe信息性太强而不一定符合之后数据。(见In[59~60],Out[96])
- 关于特征选择,提升算法的基础学习器是树,树根据信息熵划分,那么需要尽可能找到一些与目标变量之间互信息较大的特征,根据作图发现:销量呈现出年周期性,按日期平均的销量呈现出周周期性,那么合理猜测滞后接近一年和一周的整数倍的特征含有较大的互信息且比较重要,Out[62]、Out[96]和Out[97]证明了这一猜测。
- 那么是不是互信息较小特重要度小的特征应该去掉呢,我认为不是,即使存在严重泄露的时候,感想3对应的特征互信息也很小,在特征重要度中也很低,但确实显著影响模型smape。笼统地说,模型效果取决于模型特征的配合,一些互信息较小的特征,若能促进树的进一步划分,将对模型有举足轻重的贡献。
- 关注包的选择:Sklearn、XGBoost、lightGBM、CatBoost都可实现提升算法,似乎后三者计算损失函数采用了泰勒定理用一阶导数和二阶导数来近似,加快了计算。而计算效率按大家经验和我粗略的感知似乎CatBoost更快,同时我还觉得CatBoost调参负担小一点,不需怎么调参即可得到尚可的结果。似乎lightGBM、CatBoost可处理分类变量而Sklearn、XGBoost需要预处理之后才能灌入包。Sklearn似乎不能容忍数据中含有空值,而后三个包可以允许。
- 关于损失函数的选择:自带损失函数我本想选MAPE,MAPE关注误差百分比,契合竞赛的度量函数,奈何其更新太慢,设置远超1的学习率训练训练仍难以得到相当结果,于是作罢。想尝试采用平均的平方百分误差误差来训练会怎么样,不过catboost推荐用c++来构造损失函数,我暂时不掌握c++,暂时作罢。
- 设置用2013、2014年数据构造特征,2015、2016年数据用于训练事实上能得到更好效果(这时2017q1的smape可13.27),但线性插值的数据点将减少,2018年第一季度实际销量不知道的前提下不易说明预测smape的范围。
4.代码
5.图片
代码Out89部分生成的图片未能在博客显示,截图呈现。